体積を求める
体積を数値積分で求めることを考えてみましょう。 ここでは球の体積を求めること
を考えます。
まず、 高校の数学3の復習です。 平面に半径1の円を描き、 それをX軸もしくはY
軸について回転させれば、半径1の球が出来上がります。したがって、この性質を
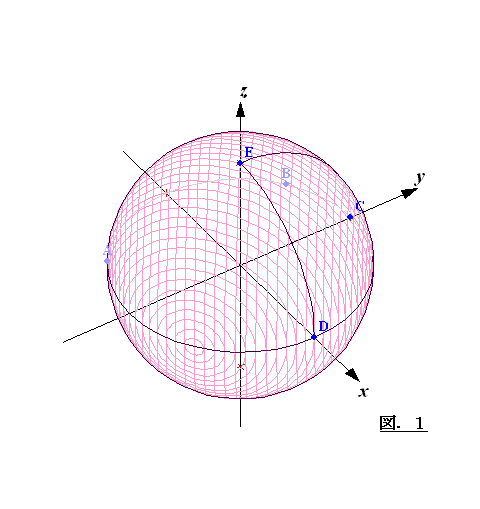
使えば、高校の積分のレベルでも球の体積を計算できます( 図1参照、フリーソフト
のFunctionviewで作成)。

それでは、 球の体積を求めるための基本的な積分式を書いてみましょう。 まず、
球の式は以下のようになります。 そして、 積分式はXとYに関する二重積分になり
ます。Yについての積分範囲に注意してください。 Xのように0から1ではなく、0か
ら円の境界線、(1−X2)1/2 までとなります。
球の式: X2+Y2+Z2=1→Z=(1−X2−Y2)1/2
積分式: V=8∫∫(1−X2−Y2)1/2 dXdY (8分の1球の体積X8)
上記の積分式は、 体積を求める数値積分のベースにはなりますが、解析的に計
算するのは容易ではありません。 そのため、最初に説明したように回転体の体積
を求めるやり方で計算してみます。
薄い円柱の体積: ΔV=π( hi )2 ΔXi
上図において、短冊状の部分(赤い斜線部)をX軸について回転させると薄い円柱
ができます。 同様にして他の短冊部分も回転させ全部足し合わせれば、結果とし
て球になります。 これを積分式の形で表すと以下のようになります。円周上の点の
Y座標が上図の短冊の高さに相当します。
円の式: X2+Y2=1→Y=(1−X2)1/2
積分式: V=2π∫(1−X2)dX=4π/3 (半球の体積X2)
ここで、積分の範囲は0から1までです。
半径1の球の体積は4π/3ということになります。 よって、 半径Rの任意の球の体
体積は4πR3/3となります。
次に、球座標を使って球の体積を計算してみます。 その前に、 球座標について説
明します。たとえば、地球上から発された電波は、宇宙に比べれば地球のサイズ
がはるかに小さいため(地球を電波の点源として扱ってもいい)、 球面状に広がっ
ていきます。 また、 マイクなどの音源から出た音波も球面状に広がっていきます。
このように互いに直交する直線的な座標で物理現象を表現するよりも、 球面上
の線と半径方向の線で構成された座標で表現した方が、記述が簡単になる場合
があります。 理系を目指す受講生の方は球座標にも慣れるようにしてください。
一般的なXYZ座標からの球座標への変換式は以下のようになります。
X=R COSθ SINφ
Y=R SINθ SINφ
Z=R COSφ
ここで、θとφは以下のように取りました(図3参照)。
球座標での微小体積を考えましょう(図4参照、Functionviewで作成)。
微小体積 を考えているので上図において線分OAの長さをRとすると、 微小な変化
AEはΔRとなります。 また、 φ方向の微小な変化ADは R にΔφをかけたものに
なります。そしてθ方向の微小な変化はABですが、 この場合、X-Y平面上に投影
した線分MNの長さがABの長さに等しいということに注意すれば、 線分OMにΔ
θをかけたものであることが判ります( 角MONの大きさと角AOBの大きさは同じで
はない)。よって、球座標における微小体積は以下のように表現できます。
R 方向の微小変化: ΔR
θ方向の微小変化: R Δθ SINφ
φ方向の微小変化: R Δφ
球座標における微小体積: R2 SINφΔR ΔθΔφ
上記の微小体積を球全体にわたって積分すれば球の体積を計算できます。ただ
し、積分自体は三重積分になります。以下に、その積分式を示します。
積分式: V=∫∫∫R2 SINφ dR dθdφ=4π/3
ここで、積分の範囲はRが0から1、θが0から2π、そして、φが0からπまでです
。この積分式の場合は、変数を分離して積分できるため簡単に計算できます。
最後に、球の体積を求めるために数値積分にトライしてみましょう。 微小な直方体
をたくさん作って足し合わせるだけです。 以下に、 十進BASICのプログラムを示し
ます。
計算している微小体積の底面のセンター座標の位置が、 原点Oから1以上離れて
いるものについて体積計算に含めないことで境界条件を考慮しています( 高さの
値が虚数にならないようにしている)。
以下はその計算結果です。二列目の数値は組み込まれているパイの値を使って計
算した値です。
X方向、 Y方向ともに100分割されているということは、 10000の微小直方体の
体積を足し合わせていることを意味します。
以下の図はドーナツ型の立体図形です。この体積と表面積を求めてみてください(
図5参照、Functionviewで作成)。
ドーナツ型の図形の場合は、 球座標よりもトーラス座標の方が計算をする上で便
利かもしれません(図6参照、Functionviewで作成)。 線分OAの長さRは一定です
。 したがって、トーラス内の任意の点の位置は、角AOBのθ、角CADのφ、 そして
線分ACの長さ r で指定することになります。
ITER( トカマク型核融合装置の国際的な研究組織)が建設している実験装置内で
発生するプラズマの形状や、 身近な所では、一般家庭やオフィスで使われている
丸型の蛍光灯内の放電プラズマの形状もドーナツ型の形状をしています。 将来、
上記のような分野に進みたいと思っている方は、 トーラス座標についてもよく勉強
しておいてください。
球座標を使った球の体積を求める三重積分は、 別名、体積積分とも言いますが、
その例をいくつか紹介します(物理や化学などのテーマも含めて)。